MindSpore专题——第五章、网络构建

发表于 2024-08-14 更新于 2024-08-16 分类于专题，机器学习， Mindspore ，基本概念阅读次数： Waline：本文字数： 1.5k 阅读时长 ≈ 6 分钟

网格构建

神经网络模型是由神经网络层和Tensor操作构成的，mindspore.nn提供了常见神经网络层的实现，在MindSpore中，Cell类是构建所有网络的基类，也是网络的基本单元。一个神经网络模型表示为一个Cell，它由不同的子Cell构成。使用这样的嵌套结构，可以简单地使用面向对象编程的思维，对神经网络结构进行构建和管理。

下面我们将构建一个用于Mnist数据集分类的神经网络模型。

定义模型类

当我们定义神经网络时，可以继承nn.Cell类，在__init__方法中进行子Cell的实例化和状态管理，在construct方法中实现Tensor操作。

class Network(nn.Cell):
    def __init__(self):
        super().__init__()
        self.flatten = nn.Flatten()
        self.dense_relu_sequential = nn.SequentialCell(
            nn.Dense(28*28, 512, weight_init="normal", bias_init="zeros"),
            nn.ReLU(),
            nn.Dense(512, 512, weight_init="normal", bias_init="zeros"),
            nn.ReLU(),
            nn.Dense(512, 10, weight_init="normal", bias_init="zeros")
        )

    def construct(self, x):
        x = self.flatten(x)
        logits = self.dense_relu_sequential(x)
        return logits


model = Network()
print(model)

Network<
  (flatten): Flatten<>
  (dense_relu_sequential): SequentialCell<
    (0): Dense<input_channels=784, output_channels=512, has_bias=True>
    (1): ReLU<>
    (2): Dense<input_channels=512, output_channels=512, has_bias=True>
    (3): ReLU<>
    (4): Dense<input_channels=512, output_channels=10, has_bias=True>
    >
  >

我们构造一个输入数据，直接调用模型，可以获得一个十维的Tensor输出，其包含每个类别的原始预测值。

model.construct()方法不可直接调用。

这里出现了很多很抽象的概念好像一下子让机器学习变成了一个黑盒子，实际上，我们观察上面的代码，很容易可以从中看出一些结构来，下面记录一下我这个初学者的理解。

首先搬出一幅经典的图像

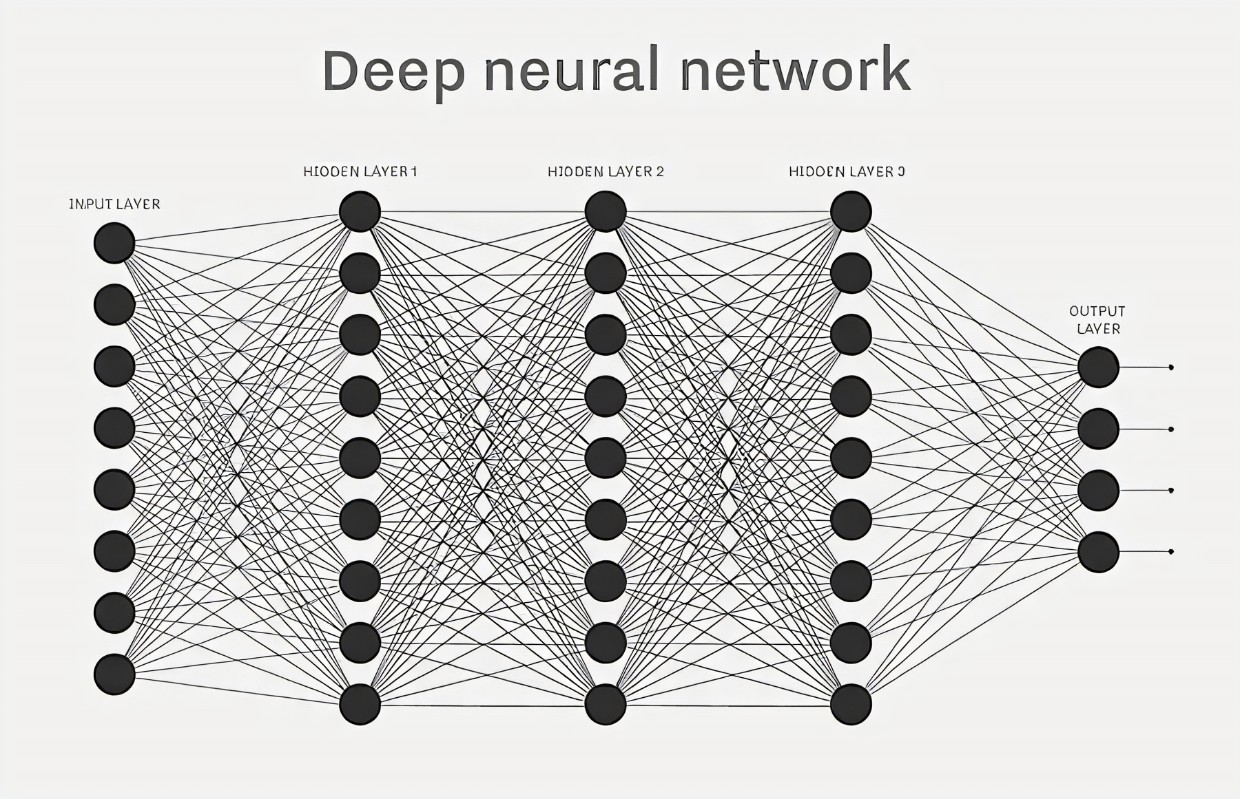
这幅图形象的描述了上面的过程。其中

这里开始的inputLayer就是我们的输入数据，中间连的密密麻麻的线就是上面结构输出中的Dense，可以观察到我们分别有\[784\rightarrow 512\rightarrow512\rightarrow10\]四层这样的全连接。最初的784也和28*28对应了起来。即我们每一个像素点都是一个参数，为最初输入的一个点，最后输出的则是代表数字概率的10个参数，最终我们会选择一个最接近的参数。这里的变量名用logits（不确定是否标准，但这里是这么用的）

下面是一些展示调用的代码

X = ops.ones((1, 28, 28), mindspore.float32)
logits = model(X)
# print logits

print(Tensor(logits))
pred_probab = nn.Softmax(axis=1)(logits)
y_pred = pred_probab.argmax(1)
print(f"Predicted class: {y_pred}")

读者可以试着运行几次，由于给出数据全是1，代表全黑或全白。因此输出是杂乱的。但可以观察到，我们最终的预测值为最大的值的标签。

下面官网上给出了一些模型层次的解释，来看看。

模型层

本节中我们分解上节构造的神经网络模型中的每一层。首先我们构造一个shape为(3, 28, 28)的随机数据（3个28x28的图像），依次通过每一个神经网络层来观察其效果。

1 2	input_image = ops.ones((3, 28, 28), mindspore.float32) print(input_image.shape)

(3, 28, 28)

nn.Flatten

实例化nn.Flatten层，将28x28的2D张量转换为784大小的连续数组。

1
2
3

flatten = nn.Flatten()
flat_image = flatten(input_image)
print(flat_image.shape)

(3, 784)

这里可见flatten打平只是打平第一维以外即输入数据样例外的维度，如果说初始数据是一个结构体数组，那Flatten的作用就是将其变为一个一维数组的数组。

nn.Dense

nn.Dense为全连接层，其使用权重和偏差对输入进行线性变换。

1
2
3

layer1 = nn.Dense(in_channels=28*28, out_channels=20)
hidden1 = layer1(flat_image)
print(hidden1.shape)

(3, 20)

这里注意到有两个额外的参数即权重和偏差。也就是说下面每一层的节点就是上一层节点的带权和加上一个常数。

nn.ReLU

nn.ReLU层给网络中加入非线性的激活函数，帮助神经网络学习各种复杂的特征。

1
2
3

print(f"Before ReLU: {hidden1}\n\n")
hidden1 = nn.ReLU()(hidden1)
print(f"After ReLU: {hidden1}")

Before ReLU: [[-0.04736331  0.2939465  -0.02713677 -0.30988005 -0.11504349 -0.11661264
   0.18007928  0.43213072  0.12091967 -0.17465964  0.53133243  0.12605792
   0.01825903  0.01287796  0.17238477 -0.1621131  -0.0080034  -0.24523425
  -0.10083733  0.05171938]
 [-0.04736331  0.2939465  -0.02713677 -0.30988005 -0.11504349 -0.11661264
   0.18007928  0.43213072  0.12091967 -0.17465964  0.53133243  0.12605792
   0.01825903  0.01287796  0.17238477 -0.1621131  -0.0080034  -0.24523425
  -0.10083733  0.05171938]
 [-0.04736331  0.2939465  -0.02713677 -0.30988005 -0.11504349 -0.11661264
   0.18007928  0.43213072  0.12091967 -0.17465964  0.53133243  0.12605792
   0.01825903  0.01287796  0.17238477 -0.1621131  -0.0080034  -0.24523425
  -0.10083733  0.05171938]]


After ReLU: [[0.         0.2939465  0.         0.         0.         0.
  0.18007928 0.43213072 0.12091967 0.         0.53133243 0.12605792
  0.01825903 0.01287796 0.17238477 0.         0.         0.
  0.         0.05171938]
 [0.         0.2939465  0.         0.         0.         0.
  0.18007928 0.43213072 0.12091967 0.         0.53133243 0.12605792
  0.01825903 0.01287796 0.17238477 0.         0.         0.
  0.         0.05171938]
 [0.         0.2939465  0.         0.         0.         0.
  0.18007928 0.43213072 0.12091967 0.         0.53133243 0.12605792
  0.01825903 0.01287796 0.17238477 0.         0.         0.
  0.         0.05171938]]

注意到，这里首次提出非线性运算的概念，也就是说，在这之前，运算都是线性的，这一步显然比较复杂，也不谈论。

nn.SequentialCell

nn.SequentialCell是一个有序的Cell容器。输入Tensor将按照定义的顺序通过所有Cell。我们可以使用SequentialCell来快速组合构造一个神经网络模型。

seq_modules = nn.SequentialCell(
    flatten,
    layer1,
    nn.ReLU(),
    nn.Dense(20, 10)
)

logits = seq_modules(input_image)
print(logits.shape)

(3, 10)

注意看代码，对于这里的代码最好都不要跳过，也不要深究实现原理（新手），可见这里依次调用了上面的所有步骤，是对这一流程的封装。

nn.Softmax

最后使用nn.Softmax将神经网络最后一个全连接层返回的logits的值缩放为[0, 1]，表示每个类别的预测概率。axis指定的维度数值和为1。

1 2	softmax = nn.Softmax(axis=1) pred_probab = softmax(logits)

官网文档已经非常清楚了。还有不懂可以跑跑代码

模型参数

网络内部神经网络层具有权重参数和偏置参数（如nn.Dense），这些参数会在训练过程中不断进行优化，可通过 model.parameters_and_names() 来获取参数名及对应的参数详情。

print(f"Model structure: {model}\n\n")

for name, param in model.parameters_and_names():
    print(f"Layer: {name}\nSize: {param.shape}\nValues : {param[:2]} \n")

通过这一代码可以查看权重参数和偏置参数，这一代码应该是十分常见并且常用的。