abc354

发表于 更新于 分类于 ， ， 阅读次数： Waline： 本文字数： 1.9k 阅读时长 ≈ 7 分钟

C - AtCoder Magics

题意

高桥有 \[N\] 张纸牌，来自纸牌游戏 "AtCoder Magics"。其中的 \[i\] 张卡将被称为 \[i\] 张卡。每张卡都有两个参数：强度和成本。卡片 \[i\] 的强度为 \[A_i\] ，成本为 \[C_i\] 。

他不喜欢弱牌，所以他会弃掉它们。具体来说，他会重复下面的操作，直到无法再进行为止：

  • 选择两张牌 \[x\] 和 \[y\] ，即 \[A_x > A_y\] 和 \[C_x < C_y\] 。弃牌 \[y\] 。

可以证明，当无法再进行操作时，剩下的牌的集合是唯一确定的。请找出这组牌。

题解

对双键值进行排序，然后判断当前的成本是否高于前面的就好，似乎这一题并不存在相同成本不同强度的淘汰数据较弱，所以注释掉也没关系

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
void slove() {
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i].x.y>>a[i].x.x,a[i].y = i;

	sort(a+1,a+1+n);
	// for(int i=1;i<=n;i++) cout<<a[i].y<<endl;

	std::vector<int> ans;
	int mx = 0;
	for(int i=1;i<=n;i++){
		int j = i;
		int t = 0;
		if(a[j].x.y > mx) ans.push_back(a[j].y);
		t = max(t, a[j].x.y);
		// while(j<n && a[j+1].x.x == a[j].x.x){
		// 	if(a[j].x.y > mx) {
		// 		// cout<<a[j].y<<endl;
		// 		ans.push_back(a[j].y);
		// 	}
		// 	t = max(t, a[j].x.y);
		// 	j++;
		// }
		mx = max(t,mx);
		// cout<<mx<<endl;
		i = j;
	}
	sort(all(ans));

	cout<<ans.size()<<endl;

	for(int idx: ans) cout<<idx<<' ';
		cout<<endl;
}

D - AtCoder Wallpaper

题意

AtCoder 的壁纸图案可以在 \(xy\) (平面)上表示如下：

  • 该平面由以下三种线段划分：
    • \[x = n\] (其中 \(n\) 为整数)
    • \[y = n\] (其中 \(n\) 为偶数)
    • \[x + y = n\] (其中 \(n\) 为偶数)
  • 每个区域都涂成黑色或白色。沿着其中一条线相邻的两个区域被涂成不同的颜色。
  • 包含 \[(0.5, 0.5)\] 的区域被涂成黑色。

下图显示了图案的一部分。

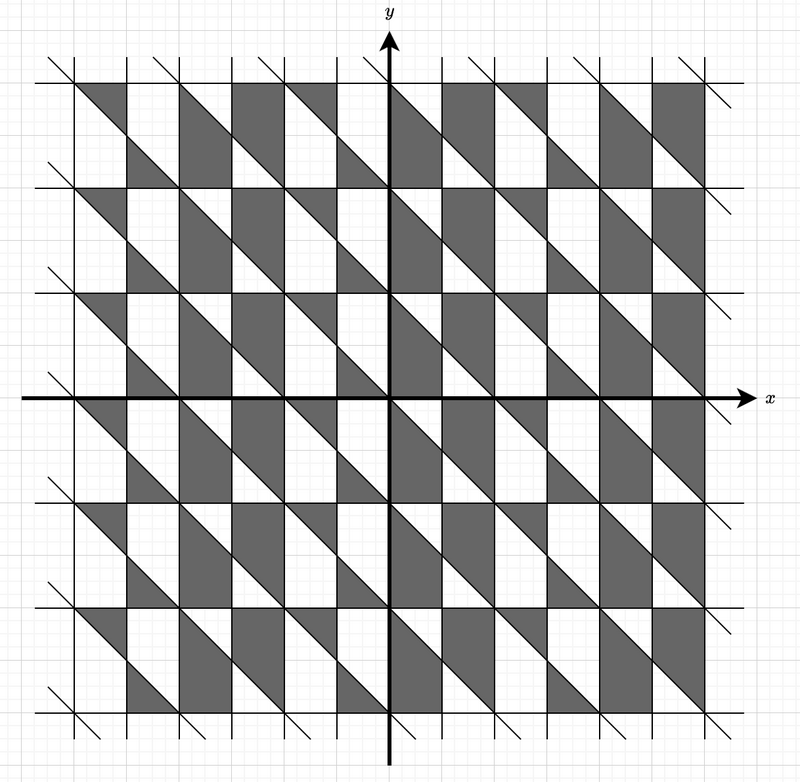
给你整数 \[A, B, C, D\] 。考虑一个边平行于 \[x\] - 和 \[y\] - 轴的矩形，它的左下顶点在 \[(A, B)\] ，右上顶点在 \((C, D)\) 。计算该矩形内部涂黑区域的面积，并打印出该面积的两倍。

可以证明输出值将是一个整数。

题解

构造题，一个好的数学思维，构造模式是十分重要的，abc上就经常会出现这样的题。

对于该题来讲，我们观察到明显的周期重复，对一个2*4的小矩形图案的不断重复，因此我们只需要枚举该图案的某一格在选中的矩形中重复了多少次即可。

加上偏移量以确保两个数的正负号问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void slove() {
	int a,b,c,d;

    cin>>a>>b>>c>>d;

    ll ans = 0;
    for(int i = 0; i<2 ; i++){
        for(int j = 0; j<4; j++){
            ll x1 = (a - j + 3 + B)/4, x2 = (c - j + 3 + B)/4;
            int coux = x2 - x1;
            ll y1 = (b - i + 1 + B)/2, y2 = (d - i + 1 + B)/2;
            int couy = y2 - y1;
            ans += coux * couy * p[i][j];
        }
    }

    cout<<ans<<endl;
}

E - Remove Pairs (atcoder.jp)

题意

高桥和青木正在玩一个使用 \[N\] 张卡片的游戏。 \(￥\) 这张牌的正面写着 \[A_i\] ，背面写着 \[B_i\] 。最初， \[N\] 这张牌摆在桌上。高桥先出，两位玩家轮流进行以下操作：

  • 从桌上选择一对正面数字相同或背面数字相同的牌，然后从桌上拿走这两张牌。如果没有这样的一对牌，玩家就不能进行操作。

最先无法进行操作的玩家输，另一名玩家赢。如果双方都以最佳方式出牌，谁会赢？

题解

乍一看是一道非常困难的博弈题，实际尝试下来也确实如此。但是\[N \leq 18\]!

于是直接暴力位dp即可

但是这里需要注意一下状态转移，根据博弈论，我们可以知道只要下一状态存在先手必输则当前状态位先手必胜，我们用0表示必输，1表示必胜。同时很容易观察到，我们并不是从较小的卡片数到较高的卡片数枚举的，因此我们需要对当前枚举的两张卡通过当前状态进行限制。以保证从小状态向大状态转移（这也可以说显然的，因为必须保证有卡才能取卡）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
void slove() {
	cin>>n;
	for(int i=0;i<n;i++)cin>>a[i].x>>a[i].y;


	for(int i=0;i<(1<<n);i++){
		for(int x=0;x<n;x++)
		{
			for(int y=x+1;y<n;y++){
				if((i >> x & 1) && (i >> y & 1) &&
				 ((a[x].x==a[y].x) || (a[x].y == a[y].y))){
					f[i] |= !f[i^(1<<x)^(1<<y)];
					// cout<<i<<' '<<x<< ' '<<y<<' '
					// 	<<(i^(1<<x)^(1<<y))<<' '<<f[i^(1<<x)^(1<<y)]<<endl;
					// cout<<f[i]<<endl;
				}
			}
		}
	}

	if(f[(1<<n)-1]) cout<<"Takahashi\n";
	else cout<<"Aoki\n";
}

F - Useless for LIS (atcoder.jp)

题意

给你一个长度为 \[N\] 的整数序列 \[A\] 。

对于每个 \[t = 1, 2, \dots, N\] ，判断 \[A_t\] 是否包含在 \[A\] 的最长递增子序列中。

这里，当且仅当以下条件成立时， \[A_t\] 才包含在 \(A\) 的最长递增子序列中：

  • 设 \[L\] 是 \[A\] 的最长递增子序列的长度。存在一个严格递增整数序列 \[i = (i_1, i_2, \dots, i_L) (i_1 < i_2 < \dots < i_ L)\] ，其中每个元素都介于 \[1\] 与 \[N\] 之间，且满足以下所有条件：

    • \[A_{i_1}<A_{i_2}<\dots<A _{i _L}\] .
    • \[i_k = t\] 为某个 \[k (1 \leq k \leq L)\] 。

给你 \(T\) 个测试用例，请逐个求解。

什么是最长递增子序列？

序列 \(A\) 的子序列是指从 \(A\) 中提取一些元素而不改变顺序所得到的序列。

序列 \(A\) 的最长递增子序列是 \(A\) 的子序列，它以最大可能的长度严格递增。

题解

求不包含在样最长上升子序列中的数的下标集合

回顾以下LIS是如何求的，通过dp求解以当前这个数为结尾的LIS最长值

这个dp需要快速找到前面比他小的数当中的最大长度，很简单，我们只需要改变一下状态表示，并且通过线段树查询一下最大值即可。

可以很简单注意到对于这样一个dp，我们只需要正序和反序均做一下dp即可达成“判断该数是否存在于LIS”的目标。

最后，数据范围离散化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
void push_up(Node* rt, Node* l,Node* r){
	rt->val = max(l->val,r->val);
}

void push_up(int u,Node* tr){
	push_up(tr+u,tr+(u<<1),tr+ (u<<1|1));
}

void build(int l,int r,int u,Node* tr){
	tr[u]={l,r};
	if(l==r) {tr[u].val = 0; return ;}
	int mid = l + r >> 1;
	build(l,mid,u<<1,tr); build(mid+1,r,u<<1|1,tr);
	push_up(u,tr);
	// cout<<tr[u].val<<endl;
	return ;
}

int query(int l,int r,int u,Node* tr){
	if(l <= tr[u].l && r >= tr[u].r){
		return tr[u].val;
	}else {
		int mid = tr[u].l +tr[u].r >> 1;
		int le = 0,ri = 0;
		if(l<= mid) le = query(l,r,u<<1,tr);
		if(r > mid) ri = query(l,r,u<<1|1,tr);
		return max(le,ri);
	}
}

void modify(int x,int c,int u,Node* tr){
	if(tr[u].l == tr[u].r && tr[u].l == x){
		tr[u].val = c;
		return;
	}else {
		int mid = tr[u].l + tr[u].r>>1;
		if(x <= mid) modify(x,c,u<<1,tr);
		else modify(x,c,u<<1|1,tr);
		push_up(u,tr);
		return ;
	}
}


void slove() {
	cin>>n;

	vector<int> ves;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		ves.push_back(a[i]);
	}

	sort(all(ves));
	ves.erase(unique(all(ves)),ves.end());

	for(int i=0;i<ves.size();i++){
		mp[ves[i]] = i+1;
	}

	build(1,n,1,tr);

	for(int i=1;i<=n;i++)
	{
		int mx = query(1,mp[a[i]]-1,1,tr);
		f[i] = mx+1;
		modify(mp[a[i]],f[i],1,tr);
	}

	int maxx = query(1,n,1,tr);

	build(1,n,1,tr);

	for(int i=n;i;i--){
		int mx = query(mp[a[i]]+1,n,1,tr);
		rf[i] = mx+1;
		modify(mp[a[i]],rf[i],1,tr);
	}

	// cout<<maxx<<endl;

	// for(int i=1;i<=n;i++){
	// 	cout<<f[i]<< ' ' << rf[i]<<endl;
	// }

	vector<int> ans;
	for(int i=1;i<=n;i++)
		if(f[i] + rf[i] - 1 == maxx){
			ans.push_back(i);
		}

	cout<<ans.size()<<endl;
	for(int v: ans) cout<<v<< ' ';
	cout<<endl;

	return ;
}

G - Select Strings (atcoder.jp)

题意

题解