PGStudy-EA and GA

发表于 更新于 分类于 ， 阅读次数： Waline： 本文字数： 3.3k 阅读时长 ≈ 12 分钟

EA 与 GA

首先需要阐明一下EA与GA分别代表什么

EA: Evolution Algorithm 进化算法

GA: Generation Algorithm 遗传算法

GA 与 EA 并非是相同的事物，两者是包含关系——GA被包含于EA

GA的规范形式 GA’s canonical form

  1. Representation - bit strings
  2. Parent selection - proportional to fitness
  3. Recombination - one-point crossover
  4. Mutation - bit flip
  5. Servival selection - next generation

名词定义 Definition

  • Phenotypes 表： the solutions within the original problem context 原始问题上下文中的解决方案
  • Genotypes 基因：Represent the phenotye 表示表型的编码
  • Fitness 适应度：A measure from some function 来自某个函数的度量，作为选择的基础，定义哪一个是更好的。
  • Population 种群：Collection of individual genotypes 单个基因型的集合，通常大小恒定。在进化过程中发生变化
  • Recombination 重组：A binary variation 一种二元变体，其中两个后代由两个亲本基因型创建，在词过程中混合了它们的属性
  • Mutation 突变：A unary variation performed on a single genotype对单个基因型进行的变异，这种变化是随机的
  • Survivor Selection 幸存者选择：The process of determining which individuals确定哪些个体（由其基因型代表）将在下一代种群中保留的过程

Overline

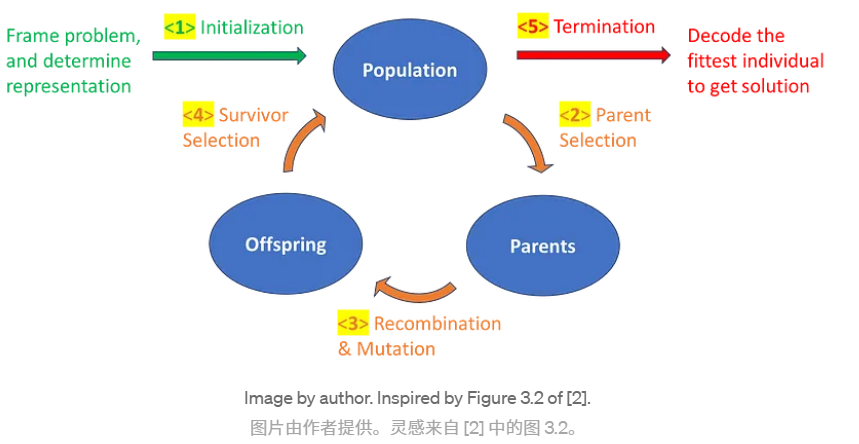
Overview

Initialization; Representation 初始化；表示法

EA goes beyond binary and permutaion representations, but we will not delve(v. 深入研究) further here.

EA存在非二进制和排列表示，但这里不做过多研究

The population will then be initialized with random copies of the appropriate genotype.

种群将由适当的基因型随机拷贝初始化种群

(why not) Binary Representation 为何不使用二进制表示

the most important reason is that mutaion is supposed to change the solution with equal probabilities, and ensure that the ensuing solution is valid.

but binary representation deviates from this. Changing a number 7 (0111) to 8 (1000) requires four bit flips, while changing it to 3 (0011) or 5 (0101) or 6 (0110) requires only one bit flip — the odds are different.

Furthermore, adjustments may be required after recombination and/or mutation, if a binary representation is used to represent a permutation. This is because each index much occur exactly once, and the resulting genotype might correspond to an invalid phenotype.

二进制的突变对不同突变方向是不公平的。这种汉明距离的差异将导致突变方向出现差异。并且由于并非每一种二进制表示都对应着实际的Representation，在每次突变重组后可能都需要进行Adjustment。

Permutation Representation 排列表示

在参考的blog中作者通过TSP问题做为典型，这里照搬。

For example, if there are 12 cities to choose from, the genotype can be [9,2,6,1,7,8,11,0,4,3,10,5].

  • [9,2,6,1,7,8,11,0,4,3,10,5]就是一种排列的基因表示
1
2
3
4
5
6
7
8
9
10
11
12
class Evolutionary:
    def __init__(self, task):
        self.task = task

    def generate_genome(self, length):
        genome = np.arange(length)
        np.random.shuffle(genome)
        return genome
        
    def generate_population(self, size, genome_length):
        population = [self.generate_genome(genome_length) for _ in range(size)]
        return population

np.arange 返回一个从1到length的numpy.ndarray

np.random.shuffle 打乱排序

Parent selection 亲本选择

In EA, the process of parent selection, variation, and survival selection happens iteratively to ensure that the population as a whole improves across generations.

在 EA 中，亲本选择、变异和生存选择的过程迭代进行，以确保种群作为一个整体在几代人中得到改善。

Roulette wheel for Parent selection 用于亲本选择的轮盘赌

A caveat is that the fitness values should be positive. Try the following yourself, and it speaks louder than a thousand words.

适应度应该是正的。

1
2
3
4
5
6
7
population=['A', 'B', 'C', 'D', 'E']
weights = [-.1, -.2, -.3, -.3, 1]
for _ in range(100):
    x = random.choices(
        population=population, weights=weights, k=2
    )
    print(x)

You will see that all negative weights have zero chance of being selected, and that a highly negative weight would be no different from a slightly negative weight.

极大概率为输出一百个[‘E’,‘E’]

并且输出大负数与输出负数的概率几乎相等

  • TPS中常见的Fitness取值为取反城市间的距离

    In TPS, one common way of representing the fitness is by negating the distance between cities.

    In this case, we need to normalize the fitness such that they are positive. This could be done by subtracting from the minimum (ie. most negative) fitness, add then adding some small epsilon to that even the worse solution has a non-zero chance of being selected.

    具体的方式是，对适应度进行归一化，并保持其为正。保持其为正的过程可以通过减去最小负数值然后加上\(\epsilon\)

  • 对于这个最小负数值也可以选择一个基线值baseline，baseline的选取会影响到个体的相对适应度和选择概率

    • 如果基线值过高，适应度的差异会被压缩，导致不同解的选择概率差异变小。
    • 如果基线值过低，适应度差异被放大，导致较优解的选择概率更高，较差解被选中的可能性更小。

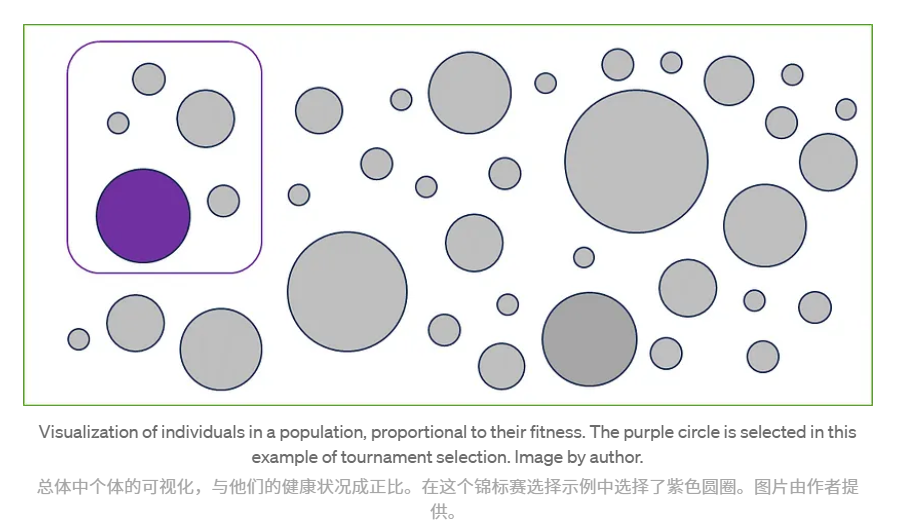
Tournament for Parent selection 亲本选拔赛

This approach is used to ensure that the fittest parents do not end up dominating most of the time.

这种方式用来确保最大适应度的亲本不会再大多数时候占据主导地位。

what happens is that a small subset of the population is randomly selected, and the fittest individual among this group gets chosen.

作者描述了下图所示的方式，通过限定范围选取最优减少全局最优的影响地位

Tournament

Implementation of coding

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Evolutionary:
    def selection(self, population, fitness_func, method='tournament'):
        if method == 'tournament':
            k = min(5, int(0.02*len(population)))
            sub_population1 = random.choices(
                population=population, k=k
            )
            sub_population2 = random.choices(
                population=population, k=k
            )
            return (
                sorted(sub_population1, key=fitness_func, reverse=True)[0], 
                sorted(sub_population2, key=fitness_func, reverse=True)[0]
            )        
        else: # roulette wheel
            min_fitness = min([fitness_func(gene) for gene in population])
            selected = random.choices(
                population=population,
                weights=[fitness_func(gene)+eps-min_fitness for gene in population],
                k=2
            )
            return tuple(selected)

Variation 变化

Variations can be unary (involving a single genotype) or binary (involving two genotypes).

变化可以是一元的，也可以是二元的，最终希望得到新的基因型并有更高的Fitness

这个过程可以借助统计数据也可以通过概率，但更多时候，通过Parent selection 与 survival selection可以确定更好的基因型

Recombination 重组

Technically, the recombination process can involve more than two parents

重组过程可能设计两个以上的父母

  • crossover 交叉

    crossover

    交叉将导致某些索引重复，而其他索引则不存在。这不能是 TSP 的解决方案。

  • Partial map crossover

    Partial map crossover

    作者提供的这个图片有些错误，在offspring栏出现了错误

    coding Implement

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    def partial_map_crossover(self, parent1, parent2):
            n = len(parent1)
            point = random.randint(0, n-1)
            child1 = list(parent1[0:point])
            for j in parent2:
                if (j in child1) == False:
                    child1.append(j)
            child2 = list(parent2[0:point])
            for j in parent1:
                if (j in child2) == False:
                    child2.append(j)
            return child1, child2

Mutation 变异

对于排列型基因，翻转、增加或减少排列的值都是不可行的

  • choose one to begining of end 选择一个数到末尾或开头
  • 交换两个数字的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
class Evolutionary:
    def __init__(self, task):
        self.task = task

    
    def partial_map_crossover(self, parent1, parent2):
        n = len(parent1)
        point = random.randint(0, n-1)
        child1 = list(parent1[0:point])
        for j in parent2:
            if (j in child1) == False:
                child1.append(j)
        child2 = list(parent2[0:point])
        for j in parent1:
            if (j in child2) == False:
                child2.append(j)
        return child1, child2
    
    
    def run_evolution(self, population_size, generation_limit=5000, fitness_limit=1e99, crossover='single', verbose=True):
        ## ... define population ...
        
        best_fitness_seen = -1e9
        for i in tqdm(range(generation_limit)):
            population = sorted(
                population, key=lambda genome: self.task.fitness(genome), reverse=True
            )
            fitness = self.task.fitness(population[0])
            
            if verbose and (fitness > best_fitness_seen):
                best_fitness_seen = fitness
                self.task.visualize(population[0], save_id=i)
            if fitness >= fitness_limit:
                break
            
            ## ... elitism; keep best individuals and variants of them ...
            
            for j in range((population_size - n_keep)//2):
                parents = self.selection(
                    population, self.task.fitness, 
                    method='tournament'
                )
                if random.random() < 0.9:
                    offspring_a, offspring_b = self.partial_map_crossover(parents[0], parents[1])
                else:
                    offspring_a, offspring_b = parents[0], parents[1]
                if random.random() < 0.9:
                    offspring_a = self.swop(offspring_a)
                    offspring_b = self.swop(offspring_b)
                next_generation += [offspring_a, offspring_b]
            population = next_generation
        
        best_genome = population[0]
        return best_genome

    
    def selection(self, ...):
        ## tournament or roulette wheel, or combination
    
    
    def shift_to_end(self, genome, num=1):
        new_genome = deepcopy(genome)
        for _ in range(num):
            a = random.sample(range(len(genome)), k=1)[0]
            ref = deepcopy(new_genome[a])
            if random.random() < 0.5:
                new_genome[1:a+1] = new_genome[:a]
                new_genome[0] = ref   # bring to first
            else:
                new_genome[a:-1] = new_genome[a+1:]
                new_genome[-1] = ref   # bring to last
        return new_genome

    
    def swop(self, genome, num=1):
        new_genome = deepcopy(genome)
        for _ in range(num):
            a, b = random.sample(range(len(genome)), k=2)
            new_genome[a], new_genome[b] = genome[b], genome[a]
        return new_genome

tqpm: 是一个快速、可扩展的Python进度条库，它可以在长循环中添加一个进度条，以显示迭代的进度。tqdm 的名字来源于土耳其语中的“tamam”（意为“完成”）。

1
2
3
4
5
6
# example
from tqdm import tqdm

for i in tqdm(range(100)):
 # 执行一些操作
 pass

Survival selection 生存选择

  • put all parents and offspring together 将父母后代放在一起，然后选取最合适的个体来生产下一代，

    这其中的问题是这种方式“稀释”了进化效应

  • mimic nature 模拟前代死亡

    这样做的问题是无法保证下一代会比前一代更好

  • select the best individual(s) from the parents. also mutate copies of them

    保留最好的前代个体并调整他们的副本,又叫“精英选择”

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    next_generation = population[:n_top]   # keep the n_top fittest individuals

    for _ in range(n_perturb):
        # select a candidate from population[:n_top]
        if np.random.random() < p_shift:
            candidate = self.shift_to_end(candidate)
        if np.random.random() < p_swop:
            candidate = self.swop(candidate)
        next_generation += [candidate]

    n_keep = n_top + n_perturb

Termination 终止

nothing important, depend on yourself

Getting The Results 取得结果

构建TSP问题的一个类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Salesman:
    def __init__(self, num_cities, x_lim, y_lim, read_from_txt=None):
        if read_from_txt:
            self.city_locations = []
            f = open(read_from_txt)
            for i, line in enumerate(f.readlines()):
                if i==num_cities:
                    break
                node_val = line.split()
                self.city_locations.append(
                    (float(node_val[-2]), float(node_val[-1]))
                )
            self.num_cities = len(self.city_locations)
            self.x_lim = np.max(np.array(self.city_locations)[:,0])
            self.y_lim = np.max(np.array(self.city_locations)[:,1])
        
        else:   # generate randomly
            self.num_cities = num_cities
            self.x_lim = x_lim
            self.y_lim = y_lim
            x_loc = np.random.uniform(0, x_lim, size=num_cities)
            y_loc = np.random.uniform(0, y_lim, size=num_cities)
            self.city_locations = [
                (x,y) for x,y in zip(x_loc,y_loc)
            ]
        self.distances = self.calculate_distances()
    
    
    def calculate_distances(self):
        distances = np.zeros((self.num_cities, self.num_cities))
        for i in range(self.num_cities):
            for j in range(i + 1, self.num_cities):
                dist = np.sqrt((self.city_locations[i][0] - self.city_locations[j][0]) ** 2 + (self.city_locations[i][1] - self.city_locations[j][1]) ** 2)
                distances[i][j] = distances[j][i] = dist
        return distances

    
    def fitness(self, solution):
        total_distance = 0
        for i in range(self.num_cities - 1):
            total_distance += self.distances[solution[i]][solution[i+1]]
        fitness = -total_distance
        return fitness
    
           
    def visualize(self, solution, save_id=None):
        n = len(solution)
        assert n == len(self.city_locations), 'The solution must correspond to all cities'
        for i, (x,y) in enumerate(self.city_locations):
            plt.plot(x, y, "ro")
            plt.annotate(i, (x, y))
        
        ordered_cities = [self.city_locations[idx] for idx in solution]
        x_coord = [x for (x,y) in  ordered_cities]
        y_coord = [y for (x,y) in  ordered_cities]
        distance = -self.fitness(solution)
        
        plt.plot(x_coord, y_coord, "gray")
        plt.title("Connected cities (%.1f) according to solution" % distance)
        if save_id is not None:
            filename = "results/plot_%03d.png" % save_id
            plt.savefig(filename, bbox_inches='tight')
            plt.close()
        else:
            plt.show()

Train and observe

1
2
3
4
5
6
7
8
salesman = Salesman(
    num_cities=30, x_lim=100, y_lim=100, read_from_txt='city_locations.txt'
)
evo = Evolutionary(salesman)
best_genome = evo.run_evolution(
    population_size=200, generation_limit=1000, crossover='pmx', verbose=True
)
salesman.visualize(best_genome)

训练与可视化

实践

问题描述：在二维平面上有一些整数坐标点组成一些联通块，在每个联通块中任意选取一个点，希望找到这些点最短环路径。

1
[(2, 12), (6, 8), (6, 16), (10, 12)]@[(5, 26), (5, 32), (6, 26), (6, 32), (7, 26), (7, 32), (8, 26), (8, 32), (9, 26), (9, 32), (10, 26), (10, 32), (11, 26), (11, 32), (5, 27), (11, 27), (5, 28), (11, 28), (5, 29), (11, 29), (5, 30), (11, 30), (5, 31), (11, 31)]@[(27, 32), (27, 38), (28, 32), (28, 38), (29, 32), (29, 38), (30, 32), (30, 38), (31, 32), (31, 38), (32, 32), (32, 38), (33, 32), (33, 38), (27, 33), (33, 33), (27, 34), (33, 34), (27, 35), (33, 35), (27, 36), (33, 36), (27, 37), (33, 37)]
1
[(10, 12), (11, 26), (27, 32)]

实现代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
import numpy as np
import random
import copy
from tqdm import tqdm
import matplotlib.pyplot as plt


n_top = 30
n_perturb = 30
p_shift = .1
p_swop = .2
eps = .1
p_up = .2
p_down = .2

class Evolutionary:
	def __init__(self,task):
		self.task = task

	def generate_genome(self,point_nums):
		genome = [[i,random.randint(0,point_nums[i]-1)] for i in range(0,len(point_nums))]
		return genome
	
	def generate_population(self, size, point_nums):
		population = [self.generate_genome(point_nums) for _ in range(size)]
		return population
	
	def partial_map_crossover(self, parent1, parent2):
		n = len(parent1)
		point = random.randint(0, n-1)
		child1 = list(parent1[0:point])
		for j in parent2:
			if any(j[0] == t[0] for t in child1) == False:
				child1.append(j)

		child2 = list(parent2[0:point])
		for j in parent1:
			if any(j[0] == t[0] for t in child2) == False:
				child2.append(j)

		return child1, child2
	
	def run_evolution(self, population_size, generation_times,fitness_limit=1e99, crossover='pmx', verbose=True):
		population = self.generate_population(population_size, self.task.point_nums)
		
		best_fitness_seen = -1e9
		for i in range(generation_times):
			population = sorted(
				population, key=lambda genome: self.task.fitness(genome), reverse=True
			)
			fitness = self.task.fitness(population[0])

			if verbose and (fitness > best_fitness_seen):
				best_fitness_seen = fitness
			if fitness >= fitness_limit:
				break

				# self.task.visualize(population[0],save_id = i)
			next_generation = population[:n_top] 

			# print(self.task.point_nums)
			for _ in range(n_perturb):
				candidate = random.choice(population[:n_top])
				# print(candidate)
				# print([len(t) for t in candidate])
				if np.random.random() < p_shift:
					candidate = self.shift_to_end(candidate)
				if np.random.random() < p_swop:
					candidate = self.swop(candidate)
					next_generation += [candidate]
				if np.random.random() < p_up:
					index = random.choice(range(len(candidate)))
					if candidate[index][1] < self.task.point_nums[candidate[index][0]] - 1:
						candidate[index][1] += 1
				if np.random.random() < p_down:
					index = random.choice(range(len(candidate)))
					if candidate[index][1] > 0:
						candidate[index][1] -= 1

			n_keep = n_top + n_perturb

			for j in range((population_size - n_keep)//2):
				parents = self.selection(
					population, self.task.fitness, 
					method='tournament'
				)
				if random.random() < 0.9:
					offspring_a, offspring_b = self.partial_map_crossover(parents[0], parents[1])
				else:
					offspring_a, offspring_b = parents[0], parents[1]
				if random.random() < 0.9:
					offspring_a = self.swop(offspring_a)
					offspring_b = self.swop(offspring_b)
				next_generation += [offspring_a, offspring_b]
			population = next_generation
        
		best_genome = population[0]
		return best_genome
	
	def selection(self, population, fitness_func, method='tournament'):
		if method == 'tournament':
			k = min(5, int(0.02*len(population)))
			sub_population1 = random.choices(
				population=population, k=k
			)
			sub_population2 = random.choices(
				population=population, k=k
			)
			return (
				sorted(sub_population1, key=fitness_func, reverse=True)[0], 
				sorted(sub_population2, key=fitness_func, reverse=True)[0]
			)  
		else: # roulette wheel
			min_fitness = min([fitness_func(gene) for gene in population])
			selected = random.choices(
				population=population,
				weights=[fitness_func(gene)+eps-min_fitness for gene in population],
				k=2
			)
		return tuple(selected)
	
	def shift_to_end(self, genome, num=1):
		new_genome = copy.deepcopy(genome)
		for _ in range(num):
			a = random.sample(range(len(genome)), k=1)[0]
			ref = copy.deepcopy(new_genome[a])
			if random.random() < 0.5:
				new_genome[1:a+1] = new_genome[:a]
				new_genome[0] = ref   # bring to first
			else:
				new_genome[a:-1] = new_genome[a+1:]
				new_genome[-1] = ref   # bring to last
		return new_genome
	
	def swop(self, genome, num=1):
		new_genome = copy.deepcopy(genome)
		for _ in range(num):
			a, b = random.sample(range(len(genome)), k=2)
			new_genome[a], new_genome[b] = genome[b], genome[a]
		return new_genome
	

class Solution:
	def __init__(self, points):
		self.points = points
		self.point_nums = []
		for i in range(len(points)):
			self.point_nums.append(len(points[i]))
		self.x_lim = np.max([np.max(np.array(t)[:,0]) for t in points])
		self.y_lim = np.max([np.max(np.array(t)[:,0]) for t in points])

	def calculate_distance(self, pointa, pointb):
		return np.sqrt((pointa[0] - pointb[0]) ** 2 + (pointa[1] - pointb[1]) ** 2)

	def fitness(self, solution):
		total_distance = 0
		# print(solution)
		for i in range(1,len(solution)):
			total_distance += self.calculate_distance(self.points[solution[i-1][0]][solution[i-1][1]],
																						self.points[solution[i][0]][solution[i][1]])
		total_distance += self.calculate_distance(self.points[solution[len(solution)-1][0]][solution[len(solution)-1][1]],
																						self.points[solution[0][0]][solution[0][1]])
		fitness = -total_distance
		return fitness
	
	def visualize(self, solution, save_id = None):
		n = len(solution)
		assert n == len(self.point_nums), 'The solution must correspond to all cities'
		for profile in self.points:
			for i, (x,y) in enumerate(profile):
				plt.plot(x, y, "o")
				plt.annotate(i, (x, y))
        
		ordered_points= [self.points[idx][pidx] for (idx,pidx) in solution]
		ordered_points.append(self.points[solution[0][0]][solution[0][1]])
		x_coord = [x for (x,y) in  ordered_points]
		y_coord = [y for (x,y) in  ordered_points]
		distance = -self.fitness(solution)
        
		plt.plot(x_coord, y_coord, "gray")
		plt.title("Connected point (%.1f) according to solution" % distance)
		if save_id is not None:
			filename = "results/plot_%03d.png" % save_id
			plt.savefig(filename, bbox_inches='tight')
			plt.close()
		else:
			plt.show()
  

points = [eval(group) for group in input().split('@')]
# print([len(t) for t in points])
printer = Solution(points)

evo = Evolutionary(printer)
best_genome = evo.run_evolution(
	population_size=100, generation_times=5000,crossover='pmx',verbose=True
)
# printer.visualize(best_genome)
print([points[idx][pidx] for (idx,pidx) in best_genome])

Ref Resource参考资料

  1. Evolutionary Algorithm — Selections Explained | by James Koh, PhD | Towards Data Science